Covering Spaces
August 2022
Introduction
These are a set of notes about covering spaces, about on the same level of difficulty/scope as Hatcher. I make no claim of originality—a lot of theorem statements are taken directly from Hatcher, or slightly modified. Other bits of content are from notes I took while taking topology at UCSB. Hopefully these notes are a bit more streamlined or easier to use for reference—all of the theorems/definitions are in convenient boxes for easy reading.
I also do a little bit more dirty work than Hatcher. For example, I frequently use the Lebesgue number lemma and pasting lemma to really show that certain lifts exist or are continuous. Proofs of these point-set topology lemmas are deferred to the last section.
Conventions
Neighborhoods are be open. We take \(S^1\subseteq \mathbb{C}\), and we often take the basepoint of \(S^1\) to be \(e^{0\cdot 2\pi i}=1\in S^1\subseteq \mathbb{C}\). All maps are continuous. We use the notation \[f: X,x \to Y,y\] to refer to a map of pointed topological spaces, i.e., a continuous map \(f:X\to Y\) which obeys \(f(x)=y\). We write \(c_x: Y \to X\) for the constant \(x\) map.
For \(\alpha: I\to X\) a path, we write \(\overline{\alpha}\) for the reversed path, i.e., \[\begin{aligned} \overline{\alpha} : I &\longrightarrow X\\ t &\longmapsto \alpha(1-x).\end{aligned}\] For two paths \(\alpha,\beta: I\to X\), we write \(\alpha \cdot \beta\) for the concatenation path, which first follows \(\alpha\) and then \(\beta\), i.e., \[\begin{aligned} \alpha \cdot \beta : I &\longrightarrow X\\ t &\longmapsto \begin{cases} \alpha(2t) & t<\frac{1}{2}\\ \beta(2t-1) & t \geq \frac{1}{2}. \end{cases}\end{aligned}\] This is easy to forget—this is backwards from the normal function composition order.
Definitions and Examples
Definition 1. A covering space of a space \(X\) (“downstairs”) is a space \(\widetilde{X}\) (“upstairs”) with a map \(p: \widetilde{X} \to X\) such that every point \(x\in X\) has an evenly covered neighborhood, i.e., a neighborhood \(V\) such that \(p^{-1}(V)\) is a disjoint union of open sets \(\widetilde{V}\) which have \[p|_{\widetilde{V}} : \widetilde{V} \to V\] being a homeomorphism.
Example 2. We claim that the real line \(\mathbb{R}\) covers the circle \(S^1\subseteq \mathbb{C}\) by the map \[\begin{aligned} p: \mathbb{R}&\longrightarrow S^1\\ t &\longmapsto e^{t 2\pi i}. \end{aligned}\]
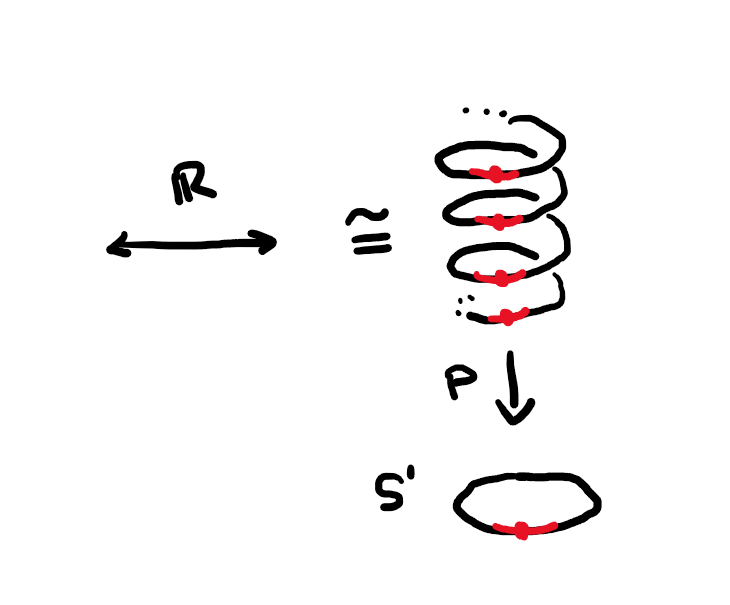
This follows because each point \(e^{\theta 2\pi i} \in S^1\) has a neighborhood \(V=\{e^{(\theta+t) 2\pi i} \operatorname{\big|}t\in (-1/2,1/2)\}\), and the preimage under \(p\) is \[\cdots, \left(\theta - 1 - \frac{1}{2},\theta-1 +\frac{1}{2}\right), \left(\theta - \frac{1}{2},\theta +\frac{1}{2}\right), \left(\theta+1 - \frac{1}{2},\theta+1 +\frac{1}{2}\right),\cdots,\] which is a disjoint collection of open subsets of \(\mathbb{R}\) which are each homeomorphically mapped to \(V\) by \(p\).
This particular covering space of \(S^1\) was very helpful in computing the fundamental group for the first time (we will reprove this machinery in greater generality soon). Our strategy was to lift maps \(f: I,0 \to S^1, 1\) to the real line \(\mathbb{R},0\), i.e., get a map \(\widetilde{f}: I,0 \to \mathbb{R},0\) such that the following diagram commutes.
This strategy comes in much greater generality with much greater utility. We’re going to try to lift (which we will define precisely later) all sorts of maps, and these theorems about lifting will help us eventually classify covering spaces of a given space.
Let’s make a definition before we get ahead of ourselves.
Definition 3. Let \(p:\widetilde{X} \to X\) be a covering space, and \(f:Y\to X\) be a map. A map \(\widetilde{f}: Y\to \widetilde{X}\) is called a lift of \(f\) if the following diagram commutes:
i.e., \(p\circ \widetilde{f} = f\).
If there is a lift, there will usually be several lifts, so we are often interested in lifts based at a certain point. That is, given a covering space \(p:\widetilde{X}\to X\) and a map \(f:X\to Y\), if we fix \(x\in X\), we set \(y=f(x)\), and we choose \(\widetilde{x}\in p^{-1}(x)\), we often look for lifts \[\widetilde{f}: Y,y \longrightarrow \widetilde{X},\widetilde{x},\] i.e., a lift \(\widetilde{f}: Y\to \widetilde{X}\) which satisfies \(\widetilde{f}(y)=\widetilde{x}\). We’ll see this when we try to lift paths.
On the other hand, it’s very common that there are no lifts at all. For example, the map \(\mathop{\mathrm{id}}_{S^1}:S^1\to S^1\) does not lift to a map \(\widetilde{f}: S^1\to \mathbb{R}\) because looking at fundamental groups/induced homomorphisms we would get
which boils down to saying that the following diagram commutes,
but the identity homomorphism does not factor through the trivial group.
Let’s look at a few more example before we prove some theorems about lifting.
Example 4. We saw already that \(\mathbb{R}\) covers \(S^1\), and it’s not hard to see that \(S^1\) covers \(S^1\) by the identity map, but \(S^1\) also covers \(S^1\) in a non trivial way. We claim \[\begin{aligned} p: S^1 &\longrightarrow S^1\\ e^{t 2\pi i} &\longmapsto e^{nt 2\pi i} \end{aligned}\] (i.e., just \(z\mapsto z^n\)) is a covering map.
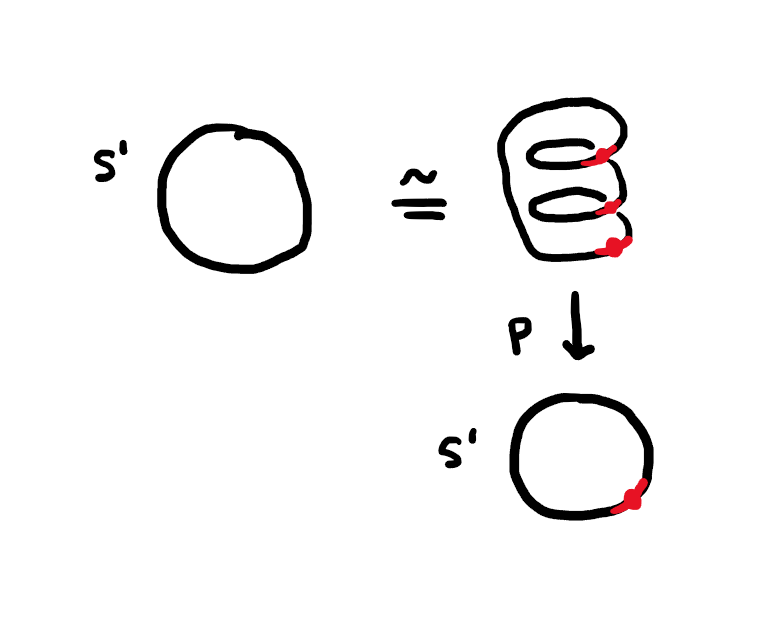
To see that this is a covering map, observe that each point \(e^{\theta 2\pi i}\) has neighborhood \(V=\{e^{\theta + t)2\pi i} \operatorname{\big|}t\in (-1/2, 1/2)\}\), and the preimage of \(V\) under \(p\) is \[A_n = \left\{e^{(\theta + t)2\pi i} \;\Big|\; t\in \left(\frac{-1}{2n}, \frac{1}{2n}\right)\right\}\] \[A_n,\; A_n + \frac{2\pi i}{n},\; \dots,\; A_n + \frac{2\pi i (n-1)}{n}.\] When you restrict \(p\) to any of these components, you indeed get a homeomorphism to \(V\).
Example 5. \(\mathbb{R}^2\) covers the cylinder \(\mathbb{R}\times S^1\) which in turn covers the torus \(S^1\times S^1\).
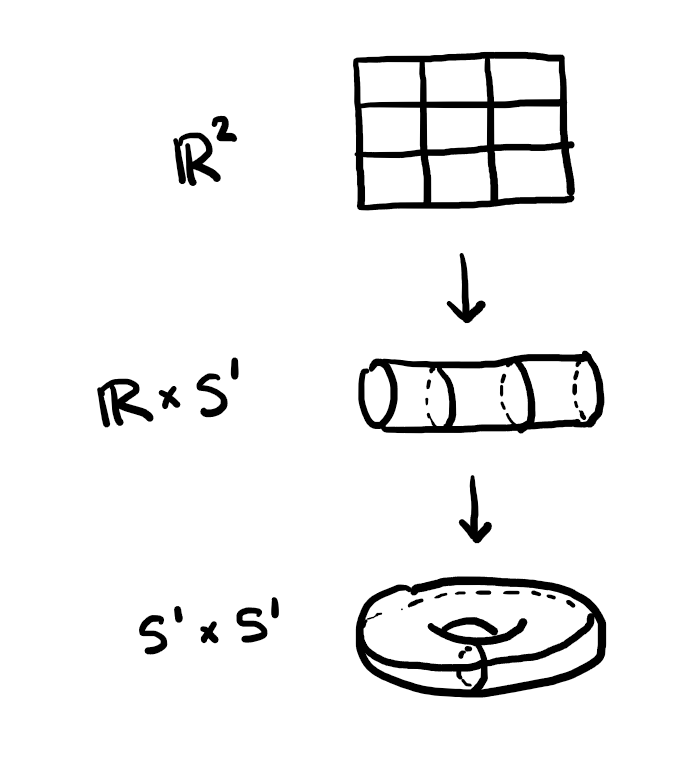
Explicitly, we can write \[\begin{aligned} &p_1: \mathbb{R}^2 \to \mathbb{R}\times S^1, \qquad (x,y)\mapsto (x,e^{y2\pi i})\\ &p_2: \mathbb{R}\times S^1 \to S^1 \times S^1, \qquad (x,e^{y2\pi i})\mapsto (e^{x2\pi i},e^{y2\pi i})\\ &p_2 \circ p_1: \mathbb{R}^2 \to S^1 \times S^1, \qquad (x,y)\mapsto (e^{x2\pi i},e^{y2\pi i}). \end{aligned}\] One can check that these are all actually covering maps because they are products of covering maps, since we can get evenly covered neighborhoods by taking products of evenly covered neighborhoods.
Lifting Theorems
Proposition 6 (Path Lifting Property). Let \(p: \widetilde{X} \to X\) be a covering space, \(f: I,0 \to X,x\) be a path, and let \(\widetilde{x}\in p^{-1}(x)\) be chosen. Then, there exists a unique lifted path \[\widetilde{f}: I,0 \longrightarrow \widetilde{X},\widetilde{x}\]
Strategy. We would like to just say \(\widetilde{f} = p^{-1}\circ f\), but in general \(p\) is not a homeomorphism and may not have continuous inverse. Instead, we use local inverses of \(p\) to keep extending to get \(\widetilde{f}\). To get local inverses, we will break \(I\) into finitely many small pieces, each which map into an evenly covered set (where we can choose open sets to have a local inverse).
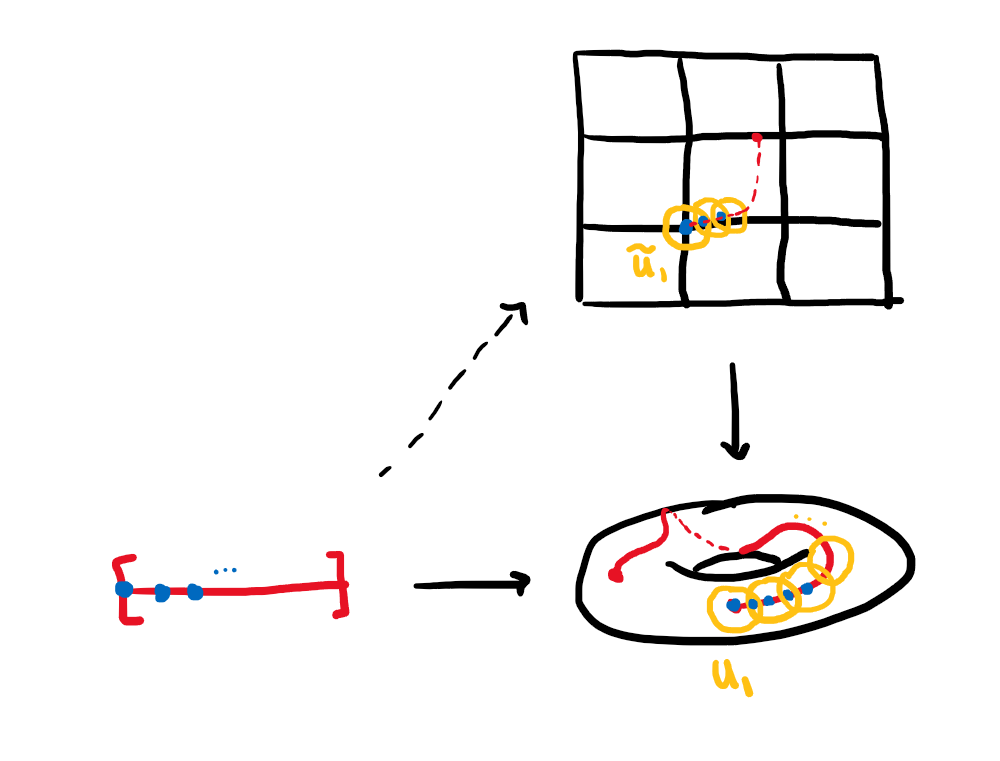
Proof. We will prove existence and uniqueness.
Existence. Since \(p:\widetilde{X}\to X\) is a covering space, each \(f(t)\in X\) has an evenly covered neighborhood \(U_t\). Then, \[\{f^{-1}(U_t) \operatorname{\big|}t\in I\}\] is an open cover of \(I\), so by the Lebesgue number lemma there exists \(\varepsilon>0\) such that each \(\varepsilon\)-ball \(B_\varepsilon(s)\subseteq I\) is contained in some \(f^{-1}(U_t)\). We choose \(n\in \mathbb{N}\) such that \(1/n < \varepsilon\). Then, we have \[I = \left[0,\frac{1}{n}\right] \cup \left[\frac{1}{n},\frac{2}{n}\right] \cup \cdots \cup \left[\frac{n-1}{n},\frac{n}{n}\right]\] where each piece has \[f\left(\left[\frac{k-1}{n},\frac{k}{n}\right]\right) \subseteq U_t\] for some \(t\in I\), and we denote this \(U_t\) by \(U_k\).
Now, we use these pieces to lift \(f\). We inductively define \(\widetilde{f_k}: [0,k/n], 0 \to \widetilde{X},\widetilde{x}\) with \(p\circ \widetilde{f_k} = f|_{[0,k/n]}\). Our base case requires us to define \(\widetilde{f_0}: [0,0], 0 \to \widetilde{X}, \widetilde{x}\), and we can just set \(\widetilde{f_0}(0)=\widetilde{x}\).
Now, assuming we’ve defined \(\widetilde{f_{k-1}}\), we define \(\widetilde{f_k}\). We choose the connected component \(\widetilde{U_k}\) of \(p^{-1}(U_k)\) that satisfies \[\widetilde{f_{k-1}}(\frac{k-1}{n}) \in \widetilde{U_k},\] and we then define \[\widetilde{f_{k}}(t) = \begin{cases} \widetilde{f_{k-1}}(t) & t\in \left[0,\frac{k-1}{n}\right]\\ \left(p|_{\widetilde{U_k}}\right)^{-1}(f(t)) & t\in \left[\frac{k-1}{n},\frac{k}{n}\right]. \end{cases}\] This map \(\widetilde{f_k}\) is well-defined because \(p\) restricted to \(\widetilde{U_k}\) is a homeomorphism and has an inverse (since \(U_k\) is chosen to be evenly covered), and by choice of \(\widetilde{U_k}\) and definition of \(\widetilde{f_{k-1}}\) we have \[\left(p|_{\widetilde{U_k}}\right)\left(\widetilde{f_{k-1}}(\frac{k-1}{n})\right) = f(\frac{k-1}{n}),\] so we can apply \((p|_{\widetilde{U_k}})^{-1}\) to get that both parts of \(\widetilde{f_{k}}\) agree on the overlap.
Since both parts are continuous and agree on overlap, by the pasting lemma (for closed sets), \(\widetilde{f_k}\) is continuous. Furthermore, it satisfies \(p\circ \widetilde{f_k} = f|_{[0,k/n]}\) because we can check on both parts of \(\widetilde{f_k}\).
Once we get to the \(n\)th step, we get our desired lift \(\widetilde{f}: I,0\to \widetilde{X},\widetilde{x}\).
Uniqueness. Suppose \(\widetilde{g}:I,0\to \widetilde{X},\widetilde{x}\) is another lift of \(f\). Our strategy to show \(\widetilde{f}=\widetilde{g}\) is to show that each time we extended \(\widetilde{f_k}\) that our hand was forced—we didn’t have any other options.
We prove that \[\widetilde{f}|_{[0,k/n]} = \widetilde{g}|_{[0,k/n]}\] by induction on \(k\). For our base case, by assumption we have \(\widetilde{f}(0)=\widetilde{g}(0)\). Now, assume that we know for \(k\) that \[\widetilde{f}|_{[0,(k-1)/n]} = \widetilde{g}|_{[0,(k-1)/n]}.\] We know that \[p \circ \widetilde{g} = f,\] and on \([(k-1)/n,k/n]\) our map \(f\) lands inside \(U_k\). Therefore, on \([(k-1)/n,k/n]\) \(\widetilde{g}\) lands in \(p^{-1}(U_k)\). Since \(\widetilde{g}\) is continuous, the image the connected set \([(k-1)/n,k/n]\) under \(\widetilde{g}\) must be connected, i.e., it must land in a single connected component of \(p^{-1}(U_k)\).
By assumption, \(\widetilde{f}((k-1)/n)=\widetilde{g}((k-1)/n)\), so the image of \([(k-1)/n,k/n]\) under \(\widetilde{g}\) must be \(\widetilde{U_k}\), the same connected component as \(\widetilde{f}\). Therefore, we can write \[p|_{\widetilde{U_k}} \circ \widetilde{f}|_{[(k-1)/n,k/n]} = p|_{\widetilde{U_k}} \circ \widetilde{g}|_{[(k-1)/n,k/n]},\] and since \(p|_{\widetilde{U_k}}\) a homeomorphism, we have \[\widetilde{f}|_{[(k-1)/n,k/n]} = \widetilde{g}|_{[(k-1)/n,k/n]}.\] Thus, we have completed our induction step, having shown \[\widetilde{f}|_{[0,k/n]} = \widetilde{g}|_{[0,k/n]}.\] After \(n\) steps, we get \(\widetilde{f}=\widetilde{g}\). Thus, the lift is unique. ◻
Remark 7. We could have tried to do this without the Lebesgue number lemma—inside each \(f^{-1}(U_t)\), pick a smaller basis neighborhood \((a_t,b_t)\) containing \(t\), and we would still have an open cover of \(I\). We would take a finite subcover, and then arrange the intervals somehow. I always find the interval arranging step a little confusing, so I’ve opted to shortcut to the Lebesgue number lemma.
Let’s see a neat application of the path lifting property.
Proposition 8. Let \(p: \widetilde{X}\to X\) be a covering space. Assume \(\widetilde{X}\) are \(X\) are both path-connected. Then, the cardinality \(|p^{-1}(x)|\) does not depend on \(x\). This constant value is called the degree of the cover.
Proof. Let \(a,b\in X\), and let \(f: I\to X\) be a path \(a\) to \(b\).
We attempt to define a bijection \(\varphi: p^{-1}(a) \to p^{-1}(b)\). For each \(\widetilde{a_i}\in p^{-1}(x)\), by the path lifting property, there exists a unique lift \[\widetilde{f_i}: I,0 \to \widetilde{X},\widetilde{a_i}\] of \(f\). Set \(\varphi(a)=\widetilde{f_i}(1)\), i.e., the other endpoint of the lifted path.
The function \(\varphi\) is well-defined by the uniqueness of the lifted path. We need to show that it is injective/surjective. Let \(\widetilde{a_1},\widetilde{a_2} \in p^{-1}(a)\), and assume that \(\varphi(\widetilde{a_1})=\varphi(\widetilde{a_2})\), so \(\widetilde{f_1}(1)=\widetilde{f_2}(1)\). Then, the reversed lifts \[\overline{\widetilde{f_1}}, \overline{\widetilde{f_2}}\] are both lifts of the reversed path \(\widetilde{f}\). Since the reversed lifts both have the same starting point, by the uniqueness part of the path-lifting property, we must have \[\overline{\widetilde{f_1}} = \overline{\widetilde{f_2}},\] so \(\widetilde{f_1}=\widetilde{f_2}\), so \(\widetilde{a_1}=\widetilde{a_2}\). Thus, \(\varphi\) is injective.
Now, we check surjectivity. Let \(\widetilde{b_j}\in p^{-1}(b)\). Then, we can lift the reversed path \(\overline{f}\) starting at \(\widetilde{b_j}\) to the lift \(\widetilde{\overline{f}_j}\), and we can check that \(\widetilde{\overline{f}_j}(1) \in p^{-1}(a)\) maps to \(\widetilde{b_j}\) under \(\varphi\). ◻
Now, we prove the more general homotopy lifting property. In general, we cannot hope to lift every single map to \(X\) to a covering space \(\widetilde{X}\). However, if we can lift a map, then we can lift an entire homotopy of it. That is, if we can specify how a homotopy lifts at time 0, we get a unique lift of the entire homotopy.
Proposition 9 (Homotopy Lifting Property). Let \(p: \widetilde{X}\to X\) be a covering space, \(F: Y\times I\to X\) a homotopy, and \(\widetilde{F_0}: Y\to \widetilde{X}\) a lift of \(f_0\). Then, there exists a unique lift \[\widetilde{F}: Y\times I \longrightarrow \widetilde{X}\] extending \(\widetilde{F_0}\).
Strategy. Let’s talk about the strategy first. For a given \(y\in Y\), we first try to lift \(F|_{N\times I}\) for a small neighborhood \(N\) of \(y\). We will use a similar argument as per the path lifting principle, and by uniqueness we will get that adjacent restrictions \[F|_{N\times I}, F|_{N'\times I}\] will agree on overlap. This will allow us to assemble the restrictions together.
We will then need to choose our small neighborhood \(N\) for which we will lift \(F|_{N\times I}\). We will choose \(N\) to be the intersection of small neighborhoods of \(y\) that come up when we try divide \(I\) into evenly covered pieces, as per the proof of the path lifting principle.
Proof. Let \(y\in Y\) be given. For each \(t\in I\), there exists an evenly covered neighborhood \(U_t\) of \(F(y,t)\). Then, there exists a basic neighborhood \(N_t\times V_t \subseteq F^{-1}(U_t)\) of \((y,t)\). The collection \[\{V_t \operatorname{\big|}t\in I\}\] is a cover of \(I\) which has subcover \(V_{t_1},\dots,V_{t_m}\). Choose a Lebesgue number \(\varepsilon>0\) for the subcover \(\{V_{t_i}\}\) and choose \(n\in \mathbb{N}\) so that \(1/n<\varepsilon\). Thus, each \[I_k = \left[\frac{k-1}{n}, \frac{k}{n}\right]\] is contained in some \(V_{t_i}\). Then, we can take \[N = \bigcap_{i=1}^m N_{t_i},\] so that for each \(k\) we have \[N\times I_k \subseteq F^{-1}(U_{t_k}).\] This is a big win—we’ve have a neighborhood \(N\) of \(y\) such that \(N\times I\) can be written as the union of sets \(N\times I_k\) which map into evenly covered sets.
Now, we’re in a good position to lift \(F|_{N\times I}\) (this is an abuse of notation—we don’t really mean the restriction because for different \(N\) this map a-priori may not be the same. Eventually, we will prove that these lifts all agree with each other, and the abuse of notation will be correct). Inductively, we define \[\widetilde{F}|_{N\times [0,k/n]},\] with our base case \(\widetilde{F}|_{N\times [0,0]}\) given by assumption, and our induction step by choosing a connected component \(\widetilde{V_{t_i}}\subseteq p^{-1}(V_{t_i})\) containing \(F(y,(k-1)/n)\) and defining \[\widetilde{F}|_{N\times [(k-1)/n,k/n]} = \left(p|_{\widetilde{V_{t_i}}}\right)^{-1}\circ F|_{[(k-1)/n,k/n]}.\] The resulting map will be well-defined by choice of \(\widetilde{V_{t_i}}\) and continuous by the pasting lemma (for closed sets).
Now, for each \(y\in Y\) we have neighborhoods \(N_y=N\) and a lift \[\widetilde{F}|_{N_y\times I} : N_y\times I \to \widetilde{X}\] with \(\widetilde{F}_{N_y\times \{0\}}\) given by assumption. We need to show that these lifts agree with each other so that they assemble into a continuous map \(\widetilde{F}: Y\times I\to \widetilde{X}\).
The collection \[\{N_y \operatorname{\big|}y\in Y\}\] forms an open cover of \(Y\). Let \(y,y'\in Y\) and let \(z\in N_y\cap N_{y'}\). Then, \[\left(\widetilde{F}_{N_y\times I}\right)_{\{z\}\times I}: \{z\}\times I\to \widetilde{X}, \qquad \left(\widetilde{F}_{N_{y'}\times I}\right)_{\{z\}\times I}: \{z\}\times I\to \widetilde{X}\] are both lifts of the path \[F|_{\{z\}\times I}: \{z\}\times I \to X\] that send \(0\mapsto \widetilde{F}_0(z)\). Thus, by the uniqueness of the path lifting property, these two maps must be the same. This just tells us that any two lifts agree on intersection, so we can get a well-defined lift \(\widetilde{F}: Y\times I \to \widetilde{X}\), which is continuous by the pasting lemma (for open sets).
Finally, our lift \(\widetilde{F}: Y\times I\to \widetilde{X}\) is unique again because each restriction to \(\{y\}\times I\) is a lift of the path \(F|_{\{y\}\times I}\), so unique by the path lifting property. ◻
Correspondence Theorem
So far, we’ve proved some theorems about lifting paths and homotopies—the essential ingredients of the fundamental group. We’re going to use these tools to study the interplay between the fundamental groups upstairs and downstairs. Let’s look at an example.
Example 10. Recall the covering \(p:S^1\to S^1\) by \(z\mapsto z^n\). Let \(\gamma:I\to S^1\) be a generator of the upstairs fundamental group, say \[\gamma(t) = e^{t2\pi i},\] and denote \(\omega\) the same map, but thought of as generating the downstairs fundamental group. Then, \[p\circ \gamma(t) = e^{nt 2 \pi i},\] so \[p_*([\gamma]) = [p\circ \gamma] = [\omega]^n.\] Under the isomorphism \(\pi_1(S^1,1)\cong \mathbb{Z}\), this tells us that \[p_*(\pi_1(S^1,1)) = n\mathbb{Z}\leq \mathbb{Z}\] By choosing different \(n\neq 0\) or by having \(\mathbb{R}\) cover \(S^1\) (corresponding to \(n=0\)), we can actually get any subgroup \(n\mathbb{Z}\leq \mathbb{Z}\) by looking at the image of the fundamental group of a covering space.
We will later see that this is example is no coincidence. These examples are leading us towards a big classification/correspondence theorem for covering spaces. We will eventually see that there is a bijection \[\{\text{covering spaces } p: \widetilde{X}\to X\}/\sim\qquad \longrightarrow \qquad \{H\leq \pi_1(X,x)\}/\sim,\] where the left equivalence relation is “isomorphism” of covering spaces and the right equivalence relation is conjugacy.
In the process, we’ll also get a powerful result telling us when we can lift any map, not just paths and homotopies.
We’ll need to prove quite a few intermediary results to build up to this correspondence and in general the connection between group theory and covering spaces. Let’s start with some quick corollaries of the homotopy lifting property.
Lemma 11. Let \(p:\widetilde{X}\to X\) be a covering space, and let \(F:I\times I\to X\) be a homotopy rel \(\partial I\) (a homotopy of paths). Given \(\widetilde{x}\in p^{-1}(F_0(0))\), \(F\) lifts uniquely to a homotopy of paths \[\widetilde{F}: I\times I \to \widetilde{X}.\]
Proof. By the path lifting property, \(F_0:I\to X\) lifts to a unique path \(\widetilde{F}_0: I\to \widetilde{X}\) starting at \(\widetilde{x}\). Then, by the homotopy lifting property, \(F\) lifts to a unique map \[\widetilde{F}: I\times I \to \widetilde{X}\] with the already defined \(\widetilde{F}_0\).
We now show that \(\widetilde{F}\) is a homotopy of paths. Since the paths \[t \mapsto F_t(0), \qquad t\mapsto F_t(1)\] are constant (because \(F\) is a homotopy of paths), and we have that \[t\mapsto \widetilde{F}_0(0), \qquad t\mapsto \widetilde{F}_0(1)\] are lifts of the respective paths, by uniqueness of path lifting we must have \(\widetilde{F}_t(0)\) and \(\widetilde{F}_t(1)\) constant. Thus, \(\widetilde{F}\) is a homotopy of paths. ◻
Proposition 12. Let \(p:\widetilde{X}\to X\) be a covering space. Then, \[p_*: \pi_1(\widetilde{X},\widetilde{x}) \longrightarrow \pi_1(X,x=p(\widetilde{x}))\] is injective.
Proof. Let \([\widetilde{f}]\in \ker{p_*}\), so \(p\circ \widetilde{f} \simeq c_x\) rel \(\partial I\). Let \[F: I\times I \to X, \qquad F_0 = p\circ \widetilde{f}, \qquad F_1=c_x\] be the homotopy. We can then lift this homotopy of paths to a homotopy of paths based at \(\widetilde{x}\), giving us \[\widetilde{F}: I\times I \to X, \qquad \widetilde{F}_0 = \widetilde{f}.\] We claim \(\widetilde{F}_1 = c_{\widetilde{x}}\). This must be the case because \(\widetilde{F}_1\) is a lift of \(c_x\) based at \(\widetilde{x}\), and so is \(c_{\widetilde{x}}\). Thus, by uniqueness \(\widetilde{F}_1 = c_{\widetilde{x}}\).
Therefore, \([\widetilde{f}]=0\) because \(\widetilde{f}\) is homotopic to \(c_{\widetilde{x}}\). Thus, \(p_*\) is injective. ◻
Proposition 4 already gives us one direction of our desired correspondence (modulo some equivalence relation), where we send a covering space \(p:\widetilde{X}\to X\) to the subgroup \(p_*\pi_1(\widetilde{X},\widetilde{x})\).
Definition 13. Let \(p:\widetilde{X}\to X\) be a covering map. Then, \(p_*(\pi_1(\widetilde{X},\widetilde{x}))\) is the subgroup of \(\pi_1(X,x)\) corresponding to the cover. This depends on choice of basepoint, and assuming \(\widetilde{X}\) is path-connected, different choices of \(\widetilde{x}\) just give conjugate subgroups.
Proposition 14. Let \(p:\widetilde{X}\to X\) be a covering space, \(\widetilde{x} \in \widetilde{X}\), \(x=p(\widetilde{x})\), and assume \(X,\widetilde{X}\) path connected. Then, \[\deg(p) = [\pi_1(X,x) : p_*(\pi_1(\widetilde{X},\widetilde{x}))]\]
Strategy. We can roughly think of covering spaces as unwrappings of a space, and the degree is how much we’ve unwrapped. Then, \(\pi_1(\widetilde{X},\widetilde{x})\) are roughly speaking the loops that weren’t broken by unwrapping (e.g., think of the cylinder covering the torus, and the two loops around the torus—one lifts to a loop, the other lifts just to a path). So the loops in \(p_*(\pi_1(\widetilde{X},\widetilde{x}))\) lift to paths ending in \(\widetilde{x}\), and the others do not. Then, the index \[[\pi_1(X,x) : p_*(\pi_1(\widetilde{X},\widetilde{x}))]\] is roughly like the number of loops based at \(x\) divided by the the number of loops that, when lifted, still end at \(\widetilde{x}\). The quotient should roughly be like the number of ways that lifted loops can end modulo redundancy—this should end up being the degree.
Proof. Let \(G=\pi_1(X,x)\) and \(H=p_*(\pi_1(\widetilde{X},\widetilde{x}))\). Our strategy is to define a bijection from \([G:H]\) to \(p^{-1}(x)\), since \(\deg(p)=|p^{-1}(x)|\). We define \[\begin{aligned} \theta: \pi_1(X,x)/H &\longrightarrow p^{-1}(x) \end{aligned}\] as follows. Given \([\alpha]H\), first lift \(\alpha\) to get \(\widetilde{\alpha}\) starting at \(\widetilde{x}\). Then, set \(\theta([\alpha])=\widetilde{\alpha}(1)\), i.e., the other endpoint of \(\widetilde{\alpha}\).
We need to show \(\theta\) is well-defined, surjective, and injective. To show well-defined, assume \([\alpha]=[\beta]\), so there is path homotopy \(F:I\times I \to X\). We can lift this homotopy to a path homotopy \(\widetilde{F}\) starting at \(\widetilde{\alpha}\). Then, \(\widetilde{F}_t(1)\) is constantly \(\widetilde{F}_0(1)=\widetilde{\alpha}(1)\) because the lift is a path-homotopy. Thus, we can get \(\theta([\beta])=\widetilde{\alpha}(1)\), and \(\theta\) is well-defined.
Next, we show \(\theta\) is surjective. Let \(\widetilde{y}\in p^{-1}(x)\). Since \(\widetilde{X}\) is path-connected, there is a path \(\widetilde{\alpha}\) from \(\widetilde{x}\) to \(\widetilde{y}\), which projects to \(p\circ \widetilde{\alpha}\), which is a loop at \(x\). Then, by the uniqueness in the path lifting property, we can get \[\theta([p\circ \widetilde{\alpha}])=\widetilde{\alpha}(1)=\widetilde{y}.\]
Finally, we show injectivity. Assume \(\theta([\alpha])=\theta([\beta])\). Then, \[\widetilde{\alpha} \cdot \overline{\widetilde{\beta}}\] is a loop at \(\widetilde{x}\), and \[[\alpha]\cdot [\beta]^{-1} = p(\widetilde{\alpha} \cdot \overline{\widetilde{\beta}}) \in H,\] so \([\alpha]H=[\beta]H\). ◻
Definition 15. Let \(P\) be a property that a topological space can have. A space \(X\) is locally \(P\) is for every \(x\in X\) and every neighborhood \(U\) of \(x\), there exists an open set \(V\) with \[x\in V\subseteq U\] such that \(V\) has property \(P\).
Example 16. We will often consider the following properties:
Locally path connected.
Locally connected.
We saw a few instances where we can lift maps—the path lifting property and the homotopy lifting property. We’re getting to a way more general result that will tell us when we can us lift all sorts of maps, and we only have to check something algebraic. The motto is that a map \(f:Y\to X\) lifts exactly when the fundamental group allows it.
Theorem 17 (Lifting Criterion for Covering Spaces). Let \(p:\widetilde{X} \to X\) be a covering space, let \(x\in X\) and \(\widetilde{x}\) a lift of \(x\). Let \(Y\) be path-connected and locally path-connected with \(y\in Y\). Given \(f: Y,y \to X,x\), there exists a lift \(\widetilde{f}: Y,y \to \widetilde{X},\widetilde{x}\) if and only if \[f_*(\pi_1(Y,y)) \subseteq p_*(\pi_1(\widetilde{X},\widetilde{x})).\]
Strategy. The hard direction is assuming \(f_*(\pi_1(Y,y))\subseteq p_*(\pi_1(X,x)))\) and showing that a lift exists. Our strategy for this is really neat. We will essentially “probe” our space with paths, and use path-lifting to figure out \(f\).
We will need to know at least one point to start off our definition of \(\widetilde{f}\), and we are given \(\widetilde{f}(y)=\widetilde{x}\). We need to figure out where to map all of the other points of \(y\). Let \(y'\in Y\). Since \(Y\) is path-connected, we have a path \(\gamma\) from \(y\) to \(y'\). Then, \(f\circ \gamma\) is a path in \(X\), and it lifts to a path in \(\widetilde{X}\). We then set \(\widetilde{f}(y')\) to be the endpoint of the lifted path.
One hurdle we will encounter is showing that this definition is well-defined, i.e., that choosing different paths \(\gamma'\) doesn’t give a different answer. This will boil down to being able to lift the loop \(f\circ (\overline{\gamma} \cdot \gamma')\). In general, we can’t always lift loops, but our condition on the fundamental groups says that we can do this.
Finally, we will need local path-connectedness to check that \(\widetilde{f}\) is actually continuous.
Proof. First, assume that a lift \(\widetilde{f}\) exists. Then, \[\begin{aligned} f &= p \circ \widetilde{f}\\ f_* &= p_* \circ \widetilde{f}_*, \end{aligned}\] so \(\mathop{\mathrm{im}}(f_*) \subseteq \mathop{\mathrm{im}}(p_*)\).
Conversely, assume that \(\mathop{\mathrm{im}}(f_*)\subseteq \mathop{\mathrm{im}}(p_*)\). We need to come up with a definition of \(\widetilde{f}\), show that it is well-defined, and finally show that it is continuous. Let \(y'\in Y\), and let \(\gamma\) be a path from \(y\) to \(y'\). Then, \(f\circ \gamma\) is a path from \(f(y)\) to \(f(y')\) in \(X\). By the path lifting property, there exists a lift of \(f\circ \gamma\), which we denote \(\widetilde{f\circ \gamma}\). Then, we set \[\widetilde{f}(y) = (\widetilde{f\circ \gamma})(1).\] A priori, this depends on \(\gamma\). To show that this is actually a function, we need to show it is well-defined.
Let \(\gamma'\) be another path from \(y\) to \(y'\). We will show that \((\widetilde{f\circ \gamma})(1) = (\widetilde{f\circ \gamma'})(1)\). Consider the loop \[(f\circ \gamma') \cdot (f\circ \overline{\gamma}) = f\circ (\gamma' \cdot \overline{\gamma}),\] whose equivalence class is in \(f_*(\pi_1(Y,y)) \subseteq p_*(\pi_1(\widetilde{X},\widetilde{x}))\). Thus, \[[f\circ (\gamma' \cdot \overline{\gamma})] = [p \circ \alpha]\] for some loop \([\alpha] \in \pi_1(\widetilde{X},\widetilde{x})\). Thus, we have a homotopy \(H: I\times I \to X\) with \(H_0 = p\circ \alpha\) and \(H_1 = f\circ (\gamma' \cdot \overline{\gamma})\). Since we have a lift \(\widetilde{H_0} = \alpha\), by the homotopy lifting property we have a lift of the homotopy \(\widetilde{H}\). Then, \(\widetilde{H}_1\) is a lift of \(f\circ (\gamma'\cdot \overline{\gamma})\). In particular, the two halves of \(\widetilde{H}_1\) are (reparameterized) lifts of \(f\circ \gamma'\) and \(f\circ \overline{\gamma}\). By the path lifting property, we then must have \[\widetilde{H}_1 = \left(\overline{f\circ \gamma'}\right) \cdot \left(\overline{\widetilde{f\circ \gamma}}\right),\] so therefore we indeed have \[(\widetilde{f\circ \gamma})(1) = (\widetilde{f\circ \gamma'})(1),\] so \(\widetilde{f}\) is well-defined.
Finally, we show that \(\widetilde{f}\) is continuous. Let \(y'\in Y\). Let \(\widetilde{U}\) be a neighborhood of \(\widetilde{f}(y')\). We can assume \(\widetilde{U}\) is small enough such that \(p|_{\widetilde{U}}\) is a homeomorphism to an open set \(U\subseteq X\).
By local path connectedness, choose an open path connected neighborhood \(V\) of \(y\) such that \(V\subseteq f^{-1}(U)\). We claim that \(\widetilde{f}(V)\subseteq \widetilde{U}\), so that \(\widetilde{f}\) is continuous at \(y'\).
Let \(y''\in V\). To evaluate \(\widetilde{f}\), let \(\gamma:I\to Y\) be a path \(y\) to \(y'\), and let \(\eta:I\to V\) be a path \(y'\) to \(y''\). Then, using the definition of \(\widetilde{f}\) and the uniqueness of path-lifting, \[\widetilde{f}(y'') = \widetilde{f\circ (\gamma\cdot \eta)} (1) = (\widetilde{f\circ \gamma}) \cdot (\widetilde{f\circ \eta})(1) = (\widetilde{f\circ \eta})(1).\] Since \(\eta\) is in \(V\subseteq f^{-1}(U)\), we actually know that the lift will be \[(p|_{\widetilde{U}})^{-1} \circ f \circ \eta\] by the uniqueness of path lifting. Thus, \[\widetilde{f}(y'') = (\widetilde{f\circ \eta})(1) = (p|_{\widetilde{U}})^{-1} \circ f \circ \eta(1) \quad \in \widetilde{U},\] so \(\widetilde{f}\) is continuous. ◻
In fact, after picking a base point that works, such lifts are unique.
Proposition 18. Let \(p:\widetilde{X}\to X\) be a covering space, and \(f:Y\to X\). If \(\widetilde{f_1},\widetilde{f_2}: Y\to \widetilde{X}\) are two lifts of \(f\) that agree at one point of \(Y\) and \(Y\) is connected, then \(\widetilde{f_1}=\widetilde{f_2}\).
Proof. Assume \(\widetilde{f_1}(y) = \widetilde{f_2}(y)\) for some point \(y\in Y\). We show that the set of points where \(\widetilde{f_1}\) and \(\widetilde{f_2}\) agree is clopen, so since it is nonempty, it must all of \(Y\) by connectedness.
Let \(y'\in Y\). Our goal is to find a neighborhood of \(y'\) where the two lifts entirely agree or disagree. Let \(U\subseteq X\) be an evenly covered neighborhood of \(f(y')\), and let \(\widetilde{U_1},\widetilde{U_2}\subseteq \widetilde{X}\) be the sheets above \(U\) containing \(\widetilde{f_1}(y'),\widetilde{f_2}(y')\) respectively. By continuity of the lifts, we can choose a neighborhood \(N\subseteq Y\) of \(y'\) such that \[\widetilde{f_1}(N)\subseteq \widetilde{U_1}, \qquad \widetilde{f_2}(N)\subseteq \widetilde{U_2}\] If \(\widetilde{f_1}(y')=\widetilde{f_2}(y')\), then \(\widetilde{U_1}=\widetilde{U_2}=\widetilde{U}\), and \[p|_{\widetilde{U}} \circ \widetilde{f_1}|_{N} = p|_{\widetilde{U}} \circ \widetilde{f_2}|_{N}\] implies by injectivity of \(p|_{\widetilde{U}}\) that \(\widetilde{f_1},\widetilde{f_2}\) agree on all of \(N\). Thus, the set of points where the lifts agree is open.
Alternatively, if \(\widetilde{f_1}(y')\neq \widetilde{f_2}(y')\), then \(\widetilde{U_1}\neq \widetilde{U_2}\), and even more they are disjoint (because they are sheets), so \(\widetilde{f_1},\widetilde{f_2}\) disagree on \(N\). Thus, the set of points where the lifts disagree is open. ◻
In our development of covering spaces and fundamental groups, we’ve finished achieving our main result on how to lift maps. Now, we turn to constructing covering spaces for each subgroup \(H\) of the fundamental group, so that we can get our desired correspondence.
For the point set topology to work out, we at least impose local path-connectedness, so that connected components and path components coincide and so that loops/fundamental group techniques are applicable. By forcing \(X\) to be locally path connected, we will automatically get \(\widetilde{X}\) locally path connected for any covering space. To get our desired correspondence, we want \(\widetilde{X}\) to be path-connected, and since it is already locally path connected, we just require connected. Thus, we will impose certain conditions on \(X\), and then study connected covering spaces.
One other technical condition we will impose on \(X\) is the following, which is satisfied by most “nice” spaces, e.g., manifolds and CW complexes.
Definition 19. A space \(X\) is semi locally simply connected (SLSC) if every \(x\in X\) has a neighborhood \(U\) such that \[i_*: \pi_1(U,x) \to \pi_1(X,x)\] is trivial.
In other words, every point \(x\) has a neighborhood \(U\) such that all loops at \(x\) in \(U\) are nullhomotopic in \(X\). Maybe a more straightforward (but strictly stronger) condition is locally simply connected, we require every point \(x\in X\) to have an open neighborhood which is simply connected (i.e., the nullhomotopies are in \(U\)).
It is straightforward to check that manifolds for locally simply connected, or even locally contractible. CW complexes require some more theory.
Let’s first see that this condition is actually necessary, so defining it isn’t a waste of time.
Proposition 20. If \(X\) has a simply connected covering space \(p: \widetilde{X}\to X\), then \(X\) is SLSC.
Proof. Let \(x\in X\). Then, \(x\) has a neighborhood \(U\) with lift \(\widetilde{U}\) such that \(p|_{\widetilde{U}}\) is a homeomorphism.
Let \(\gamma:I \to U\) be a loop at \(x\). Then, \(\gamma\) lifts to the loop \(p|_{\widetilde{U}}^{-1} \circ \gamma\), which is nullhomotopic in \(\widetilde{X}\) because \(\widetilde{X}\) is simply connected. Thus, there exists a homotopy \(h_t:I\to \widetilde{X}\) with \[h_0 = p|_{\widetilde{U}}^{-1} \circ \gamma\] and \(h_1\) being the constant loop. Then, \(p\circ h_t: I\to X\) is a homotopy in \(X\) which makes \(\gamma\) nullhomotopic. ◻
In our quest for covering spaces, we first start with getting a simply connected one. We will see later that all other covering spaces are gotten by quotienting this simply connected one.
Theorem 21. Let \(X\) be connected, locally path connected, and SLSC. Then, there exists a simply connected covering space \(p:\widetilde{X}\to X\), called a universal cover.
Strategy. We make an observation first. Fix a point \(x\in X\). In a small enough neighborhood \(U\) of \(x\) (due to the SLSC condition), points of \(U\) biject with homotopy classes of paths \(x\) to \(x'\).
Here’s the kicker though. In spaces like a torus, there are multiple homotopy classes of paths for the same point, e.g., we can loop around once or twice to get a point. This is evidence of the fundamental group being nontrivial, and it reflects how our space is somehow folded/wrapped. To unwrap the space, we copy this point several times, once for each homotopy class of paths.
As a set, we make our space \(\widetilde{X}\) the set of homotopy classes of paths, and on small sets, we transfer the topology from \(X\) to \(\widetilde{X}\). In our proof, we leave a lot of details as a sketch, since it is a little bit tedious to include all of the details.
Proof. Choose a basepoint \(x\in X\). Define the set \[\widetilde{X} = \{[\gamma] \operatorname{\big|}\gamma \text{ a path in } X \text{ starting at } x\},\] where the equivalence class \([\gamma]\) is with respect to path homotopies (fixing endpoints). We then define the map \[\begin{aligned} p: \widetilde{X} &\longmapsto X\\ [\gamma] &\longmapsto \gamma(1). \end{aligned}\] We now need to put a topology on \(\widetilde{X}\), prove that \(p\) is a covering map, and prove that \(\widetilde{X}\) is simply connected.
First, let’s give \(\widetilde{X}\) a topology. We extract data from \(X\). Define \(\mathcal{U}\) to be the collection of path-connected open sets \(U\subseteq X\) such that the induced inclusion map \(\pi_1(U) \to \pi_1(X)\) is trivial (this doesn’t depend on basepoint because \(U\) is path-connected). By the locally path connected and SLSC hypotheses, \(\mathcal{U}\) forms a basis for \(X\).
Now, for each \(U\in \mathcal{U}\) define \[U_{[\gamma]} = \{[\gamma\circ \eta] \operatorname{\big|}\eta \text{ is a path in $U$ with $\eta(0)=\gamma(1)$}\}.\] One can check that the collection of \(U_{[\gamma]}\) is a basis for topology for \(\widetilde{X}\) (i.e., can generate intersections of basic sets and the entire space). One can next check that \(p: U_{[\gamma]} \to U\) is a homeomorphism, which shows that \(p\) is not only continuous but a covering map.
Finally, we show that \(\widetilde{X}\) is simply connected. First, we show path connectedness. Let \([\gamma]\in \widetilde{X}\). Define \(\gamma_t\) by \[s\mapsto \begin{cases} \gamma(s) & s\in [0,t]\\ \gamma(t) & s\in [t,1], \end{cases}\] i.e., \(\gamma_t\) follows \(\gamma\) until \(t\), and then is stationary. Then, we have a path from the equivalence class of the constant loop \([x]\in \widetilde{X}\) to \([\gamma]\) by \[t\mapsto [\gamma_t].\] Then, we show \(\pi_1(\widetilde{X},[x]) = 0\). Let \(\widetilde{\gamma}\) be a loop in \(\widetilde{X}\) at \([x]\), so it is a lift of the path \(\gamma=p\circ \widetilde{\gamma}\). However, \(t\mapsto [\gamma_t]\) also lifts \(\gamma\) starting at \([x]\). By the uniqueness of the path-lifting property, these two paths are equal. In particular, we must have \([\gamma_1]=[x]\) for \(t\to [\gamma_t]\) to be a loop, so \([\gamma] = [x]\). Therefore, \(\pi_1(\widetilde{X},[x])=0\). ◻
Corollary 22. Let \(X\) be connected, locally path connected, and SLSC with basepoint \(x\), and let \(H\leq \pi_1(X,x)\). Then, there exists a connected covering space \(p:X_H\to X\) with \(\widetilde{x}\) lifting \(x\) and \[p_*(\pi_1(X_H,\widetilde{x})) = H.\]
Proof Sketch.. Take \(X_H\) to be a quotient of the universal covering space \(\widetilde{X}/\sim\) defined in the proof of theorem 21, where \(\sim\) is the equivalence relation defined by \([\gamma]\sim [\gamma']\) if \(\gamma' \cdot \overline{\gamma} \in H\). ◻
Now that we have existence of covering spaces corresponding to subgroups of the fundamental group, we are concerned with uniqueness. We first define the right notion equivalence.
Definition 23. Let \(p_1: \widetilde{X}_1 \to X\) and \(p_2: \widetilde{X}_2 \to X\) be two covering spaces. A morphism of covering spaces is a continuous map \(f:\widetilde{X}_1 \to \widetilde{X}_2\) such that
commutes, i.e., \(f\) respects the covering property. An isomorphism winds up being a morphism which is a homeomorphism (equivalent to a morphism with an inverse morphism).
Proposition 24. Let \(X\) be path-connected and locally path-connected with base point \(x\). Let \(p_1:\widetilde{X}_1\to X\) and \(p_2:\widetilde{X}_2 \to X\) be two connected covering spaces of \(X\) with respective basepoint lifts \(\widetilde{x_1}, \widetilde{x_2}\).
Then, \(p_1,p_2\) are isomorphic with an isomorphism \(f\) sending \(\widetilde{x_1}\mapsto \widetilde{x_2}\) iff \[{p_1}_*(\pi_1(\widetilde{X}_1,\widetilde{x_1})) = {p_2}_*(\pi_1(\widetilde{X}_2,\widetilde{x_2})).\]
Proof. Assume that \(p_1,p_2\) are isomorphic. Then, we have a homeomorphism \(f: X,x \to X,x\) such that \[p_1 \circ f = p_2,\] so the induced map \(f_*\) will be an isomorphism of \(\mathop{\mathrm{im}}(p_1)_*\) and \(\mathop{\mathrm{im}}(p_2)_*\).
Next, assume that \[{p_1}_*(\pi_1(\widetilde{X}_1,\widetilde{x_1})) = {p_2}_*(\pi_1(\widetilde{X}_2,\widetilde{x_2})).\] By the lifting criterion theorem 17, there exist a unique lifts \[\begin{aligned} \widetilde{p_1}: \widetilde{X_1}, \widetilde{x_1} &\longrightarrow \widetilde{X_2}, \widetilde{x_2}\\ \widetilde{p_2}: \widetilde{X_2}, \widetilde{x_2} &\longrightarrow \widetilde{X_1}, \widetilde{x_1}. \end{aligned}\] We claim that \(\widetilde{p_1},\widetilde{p_2}\) are inverse to each other. We look at the composition \[\widetilde{p_2} \circ \widetilde{p_1}: \widetilde{X_1},\widetilde{x}_1 \longrightarrow \widetilde{X_1},\widetilde{x}_1.\] This is a lift of \(p_1\) to \(\widetilde{X_1}\) fixing \(\widetilde{x}_1\). The identity map \(\mathop{\mathrm{id}}_{\widetilde{X_1}}\) is also a lift, so by uniqueness in proposition 18, we must have \[\widetilde{p_2} \circ \widetilde{p_1} = \mathop{\mathrm{id}}_{\widetilde{X_1}}.\] Similarly, \(\widetilde{p_1} \circ \widetilde{p_2} = \mathop{\mathrm{id}}_{\widetilde{X_2}}\), and these maps \(\widetilde{p_1},\widetilde{p_2}\) are morphisms between covering spaces \(p_1,p_2\) by construction.
Thus, \(p_1,p_2\) are isomorphic. ◻
We can then combine the previous results to get the following correspondence.
Theorem 25. Let \(X\) be locally path connected, connected, and semi-locally simply connected. Let \(x\in X\). Then, there is a bijection \[\begin{aligned} \{\text{covering spaces $p:\widetilde{X},\widetilde{x}\to X,x$}\} &\longrightarrow \{\text{subgroups of $\pi_1(X,x)$}\}\\ p &\longmapsto p_*(\pi_1(\widetilde{X},\widetilde{x})). \end{aligned}\]
Deck Transformations
We can view the universal cover of a space \(X\) as a way of getting rid of the fundamental group, making it trivial. We essentially unwrap the space.
What if we wanted to do something backwards? Start with a (maybe locally path connected) space, and make its fundamental group more complicated? In this direction, we want to wrap the space, or more precisely quotient it by a group action.
Example 26. Let’s start with an example before building the theory. The space \(\mathbb{R}^2\) is contractible (straight line homotopy), so it has trivial fundamental group. Let’s wrap it up to make it have non trivial fundamental group.
The group \(\mathbb{Z}^2\) acts on \(\mathbb{R}^2\) by translation, i.e., \[\begin{aligned} \mathbb{Z}^2 \times \mathbb{R}^2 &\longrightarrow \mathbb{R}^2\\ (n,m), (x,y) &\longmapsto (x+n, y+m). \end{aligned}\] Then, we can consider the quotient space \(\mathbb{R}^2/\mathbb{Z}^2\), i.e., \(\mathbb{R}^2/\sim\) where \((x,y)\sim (x',y')\) if and only if there exists \((n,m)\in \mathbb{Z}^2\) such that \((x+n,y+m) = (x',y')\).
We can think of this group action as wrapping \(\mathbb{R}^2\) both vertically and horizontally—one direction wraps it into a cylinder, and the second direction wraps it into a torus. We could prove that \(\mathbb{R}^2/\mathbb{Z}^2 \cong S^1\times S^1\), using the fact that \(S^1 = [0,1]/\sim\) where \(0\sim 1\). Then, we could define \[\begin{aligned} ^2/\sim \;&\longrightarrow \mathbb{R}^2/\mathbb{Z}^2\\ \overline{(x,y)} &\longmapsto \overline{(x,y)}. \end{aligned}\] using the universal property of quotient spaces, and prove that this map is a continuous bijection from a compact space to a Hausdorff space.
Then, the torus \(S^1\times S^1\) has fundamental group \(\mathbb{Z}^2\). Notice that the fundamental group is the same as the group by which we quotiented. We will see that this is not a coincidence.
We’re going to start by getting the appropriate group out of a covering space \(p: \widetilde{X}\to X\). Then, we will study quotients by sufficiently nice group actions.
Let \(X\) be a topological space, and let \(\widetilde{X}\) be the universal cover. We’ve seen how the fundamental group somehow “counts” extra points in \(\widetilde{X}\) sitting above each point in \(X\), i.e., proposition 14. In some sense, the fundamental group tells us about how \(X\) fits inside \(\widetilde{X}\). More generally, we want a group that we can associate to any covering space \(q: \widetilde{Y}\to Y\), no matter if \(\widetilde{Y}\) is the universal cover or not (i.e., a more relative notion). This group will be what we will call the group of deck transformations, which (under certain conditions) will be isomorphic to quotients of the fundamental group of \(Y\).
Definition 27. A deck transformation or covering transformation of a covering space \(p: \widetilde{X}\to X\) is an isomorphism \(f: \widetilde{X}\to \widetilde{X}\), i.e., a homeomorphism satisfying
.
The collection of deck transformations of \(\widetilde{X}\) is denoted by \(G(\widetilde{X})\), which is group under composition, called the group of deck transformations.
\(G(\widetilde{X}) \subseteq \operatorname{Homeo}(\widetilde{X})\) acts on \(\widetilde{X}\) just by \(f\cdot \widetilde{x} = f(\widetilde{x})\).
We also define a nice condition for describing when things are most convenient.
Definition 28. A normal covering space \(p: \widetilde{X}\to X\) is a covering space such that for each \(x\in X\) and each pair of lifts \(\widetilde{x},\widetilde{x}'\), there is a deck transformation \(f\) mapping \(\widetilde{x}\mapsto \widetilde{x}'\).
Now, we relate the fundamental group to deck transformations. In the process, we get a way for the fundamental group to act on a space. Then, we will be in a position to discuss the effect of quotienting by group actions on the fundamental group.
We first need a lemma about changing basepoint for covering maps.
Lemma 29. Let \(p: \widetilde{X} \to X\) be a path-connected covering space. Fix \(x\in X\), and let \(\widetilde{x},\widetilde{x}' \in p^{-1}(x)\) be two preimages. Let \(\widetilde{\gamma}\) be a path from \(\widetilde{x}\) to \(\widetilde{x}'\), and denote \(\gamma= p\circ \widetilde{\gamma}\). Then, \[p_*(\pi_1(\widetilde{X},\widetilde{x}')) = [\gamma]^{-1} \cdot p_*(\pi_1(\widetilde{X},\widetilde{x})) \cdot [\gamma]\]
Proof. We only need to show one inclusion of the equality, since the other inclusion comes from reversing \(\widetilde{x},\widetilde{x}'\). Let \(\alpha\in \pi_1(\widetilde{X},\widetilde{x})\). Then, \[\overline{\gamma} \cdot (p\circ \alpha) \cdot \gamma = p\circ (\overline{\widetilde{\gamma}} \cdot \alpha \cdot \widetilde{\gamma}),\] so indeed we get \([\gamma]^{-1} \cdot p_*([\alpha]) \cdot [\gamma] \in p_*(\pi_1(\widetilde{X},\widetilde{x}'))\) ◻
Proposition 30. Let \(p: \widetilde{X},\widetilde{x} \to X, x\) be a connected covering space of a path-connected, locally path-connected space \(X\). Let \[H = p_*(\pi_1(\widetilde{X},\widetilde{x})) \subseteq \pi_1(X,x),\] i.e., the subgroup corresponding to the covering. Then,
There exists a deck transformation \(f:\widetilde{X},\widetilde{x} \to \widetilde{X},\widetilde{x}'\) iff there exists path \(\widetilde{\gamma}\) from \(\widetilde{x}\) to \(\widetilde{x}'\) with \([p\circ \widetilde{\gamma}] \in N(H)\). Furthermore, such a deck transformation mapping \(\widetilde{x}\mapsto\widetilde{x}'\) is unique (being the lift of the covering map), and any path \(\widetilde{\gamma}\) will work.
\(p\) is normal iff \(H\trianglelefteq\pi_1(X,x)\).
\(G(\widetilde{X}) \cong N(H)/H\).
In particular, if \(p\) is normal, \[G(\widetilde{X}) \cong \pi_1(X,x)/H.\] For the universal cover, \(G(\widetilde{X})\cong \pi_1(X,x)\).
Strategy. By lemma 29, we should regard changing basepoint in the covering space as conjugating the subgroup corresponding to the cover. Then, we will see that we can change basepoint \(\widetilde{x}\mapsto\widetilde{x}'\) without changing the subgroup if there exists a deck transformation mapping \(\widetilde{x}\mapsto\widetilde{x}'\). Thus, the existence of a deck transformation says something about how conjugation does nothing, i.e., a loop is in the normalizer.
Proof of (a).. Assume there exists a deck transformation \(f:\widetilde{X},\widetilde{x} \to \widetilde{X},\widetilde{x}'\). Let \(\widetilde{\gamma}\) be any path from \(\widetilde{x}\) to \(\widetilde{x}'\), and denote \(\gamma = p\circ \widetilde{\gamma}\). We show that \([\gamma] \in N(H)\), i.e., for any \(p_*([\alpha]) \in H\), \[[\gamma]^{-1} \cdot p_*([\alpha]) \cdot [\gamma] \in H.\] By lemma 29, we can write \[[\gamma]^{-1} \cdot p_*([\alpha]) \cdot [\gamma] = p_*([\beta])\] for some \(\beta\in \pi_1(\widetilde{X},\widetilde{x}')\) for some \(\widetilde{x}'\) which is another lift of \(x\). Using the fact that \(f\) is a deck transformation, we can insert \(f\) to get \[p_*([\beta]) = p_*(f_*([\beta])),\] so we get \[[\gamma]^{-1} \cdot p_*([\alpha]) \cdot [\gamma] = p_*([\beta]) \in H.\]
Conversely, assume that there exists a path \(\widetilde{\gamma}\) from \(\widetilde{x}\) to \(\widetilde{x}'\) such that for \(\gamma=p\circ \widetilde{\gamma}\), we have \([p\circ \widetilde{\gamma}]\in N(H)\). Then, to get the desired deck transformation, we try to lift \(p:\widetilde{X},\widetilde{x}\to X,x\) to the covering space \(p:\widetilde{X},\widetilde{x}'\to X,x\). There indeed exists a lift \(f:\widetilde{X},\widetilde{x} \to \widetilde{X},\widetilde{x}'\) by the lifting criterion theorem 17 because \[H=p_*(\pi_1(\widetilde{X},\widetilde{x})) \subseteq p_*(\pi_1(\widetilde{X},\widetilde{x}')),\] since by lemma 29, for \(\widetilde{\gamma}\) a path \(\widetilde{x}\) to \(\widetilde{x}'\) and \(\gamma=p\circ \overline{\gamma}\), we have \[p_*(\pi_1(\widetilde{X},\widetilde{x}')) = [\gamma]^{-1} \cdot p_*(\pi_1(\widetilde{X},\widetilde{x})) \cdot [\gamma] = [\gamma]^{-1} \cdot H \cdot [\gamma],\] and by assumption \([\gamma]^{-1}\cdot H \cdot [\gamma] = H\) because \([\gamma]\in N(H)\).
Additionally, this deck transformation is unique, since for another deck transformation \(g\) mapping \(\widetilde{x}\mapsto \widetilde{x}'\), we have that \(g\) is also a lift of \(p:\widetilde{X},\widetilde{x}\to X,x\) to the covering space \(p:\widetilde{X},\widetilde{x}'\to X,x\), since \(p\circ g = p\). Therefore, by uniqueness in proposition 18, we must have \(g=f\). ◻
Proof of (b).. Assume \(p\) is normal. Then, for any \([\gamma]\in \pi_1(X,x)\), denote \(\widetilde{\gamma}\) the lift starting at \(\widetilde{x}\), and let \(\widetilde{x}'=\widetilde{\gamma}(1)\) its other endpoint. Since \(p\) is normal, there is a deck transformation \[f:\widetilde{X},\widetilde{x} \longrightarrow \widetilde{X},\widetilde{x}',\] so by part (a), we get \([\gamma] \in N(H)\). Therefore, \(N(H)=\pi_1(X,x)\) so \(H\trianglelefteq\pi_1(X,x)\).
Conversely, assume that \(H\trianglelefteq\pi_1(X,x)\). A priori, we should show for any \(y\in X\) and two pairs of lifts \(\widetilde{y},\widetilde{y}'\), there exists a deck transformation sending \(\widetilde{y} \mapsto \widetilde{y}'\). However, we can assume \(y=x\), since otherwise we could use lemma 29 to switch to \(y\) as our basepoint, while still getting \(H\) a normal subgroup. Additionally, we can assume \(\widetilde{y}=\widetilde{x}\) because we can compose multiple deck transformations to map between arbitrary lifts of \(x\).
Therefore, we just need to show the existence of a deck transformation mapping \(\widetilde{x}\mapsto \widetilde{x}'\). Let \(\widetilde{\gamma}\) be a path from \(\widetilde{x}\) to \(\widetilde{x}'\). Since \(H\) is a normal subgroup, we have \([p\circ \widetilde{\gamma}] \in N(H)\). Thus, by part (a) there exists the desired deck transformation. ◻
Proof of (c).. We construct a (surjective) group homomorphism \(\varphi: N(H)\to G(\widetilde{X})\), and show the kernel is \(H\). For \([\gamma]\in N(H)\), lift the loop to a path \(\widetilde{\gamma}\) starting at \(\widetilde{x}\) and define \(\widetilde{x}'=\widetilde{\gamma}(1)\). By part (a), there exists a unique deck transformation \(f\) mapping \(\widetilde{x}\mapsto \widetilde{x}'\), so define \(\varphi([\gamma]) = f\).
The function \(\varphi\) is indeed a homomorphism, since \(\varphi([\beta])\circ \varphi([\alpha])\) is still a deck transformation, and it maps \(\widetilde{x}\) to \(\widetilde{\beta\cdot \alpha}(1)\), so we must have \[\varphi([\beta])\circ \varphi([\alpha]) = \varphi([\beta][\alpha]).\]
The surjectivity of \(\varphi\) is immediate from part (a). Finally, \([\gamma]\in \ker{\varphi}\) if and only if \(\varphi([\gamma])\) maps \(\widetilde{x}\mapsto \widetilde{x}\), which occurs exactly when \([\gamma]\) lifts to a loop at \(\widetilde{x}\), i.e., \([\gamma] \in H\).
Thus, by the first isomorphism theorem \[N(H)/H \cong G(\widetilde{X}).\] ◻
The type of group action we get from covering spaces are very particular. This isn’t standard terminology, but it’s what Hatcher uses.
Definition 31. A group action \(\mu: G \to \operatorname{Homeo}(Y)\) is called a covering space action if for each \(y\in Y\), there exists a neighborhood \(U\) such that the images \(g(U)\) for all \(g\in G\) are disjoint. In other words, \(g_1(U)\cap g_2(U)\neq \emptyset\) implies \(g_1=g_2\).
One can think of this definition as saying that the orbits \(G\cdot x\) of the group action are uniformly discrete, in the sense that there is an open set of “equal size” separating each point in the orbit. Additionally, the definition implies a covering space action needs to be free, i.e., all non identity group elements have no fixed points. In particular, this means that the homomorphism \(\mu: G\to \operatorname{Homeo}(Y)\) is injective, so we might as well consider \(G\subseteq \operatorname{Homeo}(Y)\).
Proposition 32. If \(G\) has a covering space action on \(Y\), then
The quotient map \(p: Y\to Y/G\) is a normal covering space.
If \(Y\) is path-connected and locally path-connected, then \(G \cong G(Y)\), i.e., \(G\) is the group of deck transformations of the covering space \(Y\to Y/G\).
If \(Y\) is path-connected and locally path-connected, then \(G\cong \pi_1(Y/G)/p_*(\pi_1(Y))\).
Proof of (a).. We first show that \(p\) is a covering map. Let \(G\cdot y \in Y/G\). Choose \(U\) to be a neighborhood of \(y\) as given by the definition of \(G\) being a covering space action. Then, \(G\cdot U \subseteq Y/G\) has preimage \(\{g\cdot U \operatorname{\big|}g\in G\}\) which is a disjoint union of sets homeomorphic to \(U\) (since \(g\) acts as a homeomorphism, and by assumption the \(g\cdot U\) are disjoint). Thus, \(U\) is an evenly covered neighborhood, so \(p\) is a covering map.
Next, we show \(p: Y\to Y/G\) is a normal covering space. For \(y',y\in G\cdot y\), by definition there is a \(g\in G\) such that \(g\cdot y = y'\), and this \(g\) acts as a deck transformation. ◻
Proof of (b).. Identifying \(G\) as a subset of \(\operatorname{Homeo}(Y)\), we can quickly get \(G\subseteq G(Y)\). Conversely, let \(f\in G(Y)\) and \(y\in Y\). Since \(f\) is a deck transformation \(f(y)\in G\cdot y\), so there exists \(g\in G\) such that \(g\cdot y = f(y)\). By proposition 30 (a), \(f=g\) because \(Y\) is path connected and both map \(y\mapsto g\cdot y\). Thus, \(f\in G\), so \(G\cong G(Y)\) by the map that includes \(G\hookrightarrow \operatorname{Homeo}(Y)\). ◻
Note. For (b), we don’t actually have to assume \(Y\) is locally path-connected (as would suggest the hypotheses of proposition 30). Local path-connectedness helps get existence of lifts, but only path-connectedness is needed for uniqueness. We already have existence, we only needed uniqueness.
Proof of (c).. This follows from (a), (b), and proposition 30. ◻
Point-Set Topology Lemmas
I’ve collected proofs of point-set topology lemmas that are used earlier.
Lemma 33 (Lebesgue’s Number Lemma). Let \(X\) be a compact metric space, and let \(\{U_i \operatorname{\big|}i \in I\}\) be an open cover of \(X\). Then, there is a \(\delta>0\) such that every \(\delta\)-ball in \(X\) is contained in some \(U_i\). This \(\delta\) is called a Lebesgue number for the cover \(\{U_i \operatorname{\big|}i\in I\}\).
Proof. Suppose, to the contrary, that there is no such \(\delta\). Therefore, for \(\delta=\frac{1}{n}\), there exists \(x_n\in X\) with \(B_{\frac{1}{n}}(x_n)\) not contained in any \(U_i\). By compactness, take a convergent subsequence \(\{x_{n_k}\}\) converging to \(x\in X\). Since \(x\in X\), it is in some open set in the cover, say \(U_{i_0}\). Therefore, there exists \(\delta>0\) such that \(B_{\delta}(x) \subseteq U_{i_0}\).
However, we can choose \(k\in \mathbb{N}\) large so that \[d(x_{n_k}, x) < \frac{\delta}{2}\] and at the same time we can choose \(k\geq \frac{2}{\delta}\) so that \(n_k \geq \frac{2}{\delta}\). By our construction of the sequence, this means that \[B_{\frac{1}{n_k}}(x_{n_k}) \not\subseteq U_{i_0},\] but on the other hand we have \[B_{\frac{1}{n_k}}(x_{n_k}) \subseteq B_{\frac{\delta}{2}}(x_{n_k}) \subseteq B_{\delta}(x)\] because for any \(y\in B_{\frac{\delta}{2}}(x_{n_k})\), \(d(x,y)\leq d(x,x_{n_k}) + d(x_{n_k},y) < \delta\), so \(y\in B_{\delta}(x)\).
However, this gives us \(B_{\frac{1}{n_k}}(x_{n_k}) \subseteq B_{\delta}(x)\subseteq U_{i_0}\), which is a contradiction.
Thus, there does exist a \(\delta>0\) such that every \(\delta\)-ball in \(X\) is contained in some \(U_i\). ◻
Lemma 34 (Pasting Lemma for Closed Sets). Let \(A, B\) be both closed subsets of a topological space \(X\) such that \(X=A\cup B\) (\(A,B\) need not be disjoint). For \(f:X\to Y\), if \[f|_A: A\to Y, \quad f|_B: B\to Y\] are both continuous, then \(f\) is continuous.
Proof. Let \(E\subseteq Y\) be closed. It suffices to show that \(f^{-1}(E)\) is closed. We have \[\begin{aligned} f^{-1}(E) &= f^{-1}(E) \cap (A\cup B)\\ &= (f^{-1}(E)\cap A) \cup (f^{-1}(E)\cap B)\\ &= (f|_A)^{-1}(E) \cup (f|_B)^{-1}(E). \end{aligned}\] Since \(A,B\) are closed, the fact that \[(f|_A)^{-1}|(E), \quad (f|_B)^{-1}|(E)\] are closed in the subspace topologies implies that they are closed in all of \(X\) as well because they are intersections closed subsets of \(X\) with \(A,B\) (which already closed).
(This is the point of the proof—we are using the closed definition of continuity rather than the open definition because of this). ◻
Lemma 35 (Pasting Lemma for Open Sets). Let \(\{U_i\}_{i\in I}\) be an open cover of a space \(X\), and assume the function \(f:X\to Y\) is such that \[f|_{U_i}: U_i \to Y\] is continuous for all \(i\in I\). Then, \(f\) is continuous.
Proof. Let \(V\subseteq Y\) be open. Then, \[\begin{aligned} f^{-1}(V) &= \bigcup_{i\in I} f|_{U_i}^{-1}(V). \end{aligned}\] Each \(f|_{U_i}\) is continuous, so by the subspace topology \[f|_{U_i}^{-1}(V) = W_i \cap U_i\] for some open set \(W_i\). Then, \[f^{-1}(V) = \bigcup_{i\in I} W_i\cap U_i,\] so \(f^{-1}(V)\) is the union of open sets and hence open. Thus, \(f\) is continuous. ◻